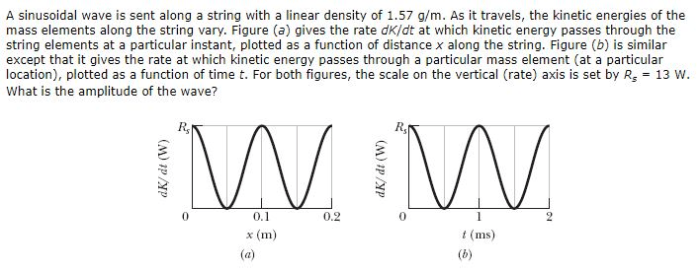
A sinusoidal wave is sent along a string, embarking on a journey that unveils the intricacies of wave propagation, interactions, and their myriad applications. This wave, characterized by its undulating shape, holds within it a wealth of physical phenomena that shape our understanding of the world around us.
From the fundamental characteristics of amplitude, frequency, and wavelength to the propagation of waves along a string, we delve into the factors that govern wave velocity and direction. Interactions with boundaries and other waves reveal the complexities of reflection, standing waves, superposition, interference, and resonance.
Characteristics of a Sinusoidal Wave: A Sinusoidal Wave Is Sent Along A String
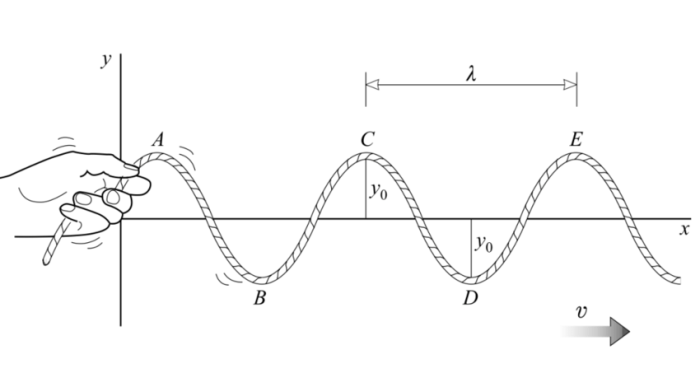
A sinusoidal wave is a type of wave that has a smooth, undulating shape that repeats itself at regular intervals. It is characterized by its amplitude, frequency, and wavelength.
The amplitude of a sinusoidal wave is the maximum displacement of the wave from its equilibrium position. The frequency of a sinusoidal wave is the number of times the wave repeats itself per unit time. The wavelength of a sinusoidal wave is the distance between two consecutive crests or troughs of the wave.
The shape of a sinusoidal wave can be represented by the following equation:
y = A sin(2πft
kx)
where:
- y is the displacement of the wave from its equilibrium position
- A is the amplitude of the wave
- f is the frequency of the wave
- t is the time
- k is the wave number
- x is the position along the wave
The wave number is related to the wavelength of the wave by the following equation:
k = 2π/λ
where λ is the wavelength of the wave.
Propagation of a Sinusoidal Wave
When a sinusoidal wave is sent along a string, the string vibrates up and down in a transverse direction to the direction of wave propagation. The wave travels along the string at a speed that is determined by the tension in the string and the mass density of the string.
The wave velocity is given by the following equation:
v = √(T/μ)
where:
- v is the wave velocity
- T is the tension in the string
- μ is the mass density of the string
The wave velocity is independent of the frequency and amplitude of the wave.
Interactions with Boundaries
When a sinusoidal wave encounters a fixed boundary, such as a wall, it is reflected back from the boundary. The reflected wave has the same amplitude and frequency as the incident wave, but it is inverted in phase. This means that the crests of the incident wave become the troughs of the reflected wave, and vice versa.
When a sinusoidal wave is reflected from a boundary, it can form a standing wave. A standing wave is a wave that is confined to a particular region of space. The standing wave is formed by the superposition of the incident wave and the reflected wave.
Interactions with Other Waves
When two sinusoidal waves of different frequencies or amplitudes interact, they can produce a variety of different effects. These effects include superposition, interference, and resonance.
Superposition is the process of adding two or more waves together to produce a new wave. The resulting wave has a shape that is determined by the shapes of the individual waves.
Interference is the process of combining two or more waves to produce a new wave that has a different amplitude than the individual waves. The amplitude of the resulting wave depends on the phase difference between the individual waves.
Resonance is the process of combining two or more waves to produce a new wave that has a larger amplitude than the individual waves. Resonance occurs when the frequency of the individual waves is equal to the natural frequency of the system.
Mathematical Representation, A sinusoidal wave is sent along a string
The mathematical equation that describes a sinusoidal wave is:
y = A sin(2πft
kx)
where:
- y is the displacement of the wave from its equilibrium position
- A is the amplitude of the wave
- f is the frequency of the wave
- t is the time
- k is the wave number
- x is the position along the wave
The following table summarizes the key equations and their applications:
| Equation | Application |
|---|---|
y = A sin(2πft
|
Describes the shape of a sinusoidal wave |
| v = √(T/μ) | Calculates the wave velocity |
| f = 1/T | Calculates the frequency of a wave |
| λ = v/f | Calculates the wavelength of a wave |
| k = 2π/λ | Calculates the wave number |
Applications
Sinusoidal waves have a wide range of applications in various fields, including:
- Signal processing
- Communication systems
- Music and acoustics
- Medical imaging
In signal processing, sinusoidal waves are used to represent signals such as sound and images. In communication systems, sinusoidal waves are used to transmit information over long distances.
In music and acoustics, sinusoidal waves are used to create sounds and to analyze the sound quality of musical instruments. In medical imaging, sinusoidal waves are used to create images of the inside of the body.
FAQ Summary
What is a sinusoidal wave?
A sinusoidal wave is a wave with a smooth, undulating shape that can be described by a sine or cosine function. It is characterized by its amplitude, frequency, and wavelength.
How does a sinusoidal wave propagate along a string?
When a sinusoidal wave is sent along a string, it travels at a speed determined by the tension and mass density of the string. The wave’s amplitude, frequency, and wavelength remain constant as it propagates.
What happens when a sinusoidal wave encounters a fixed boundary?
When a sinusoidal wave encounters a fixed boundary, it is reflected back with a change in phase. The reflected wave can interfere with the incident wave, creating standing waves.
What is superposition?
Superposition is the principle that when two or more waves overlap, the resulting wave is the sum of the individual waves. This principle is essential for understanding wave interactions, such as interference and resonance.
What are some applications of sinusoidal waves?
Sinusoidal waves have a wide range of applications, including signal processing, communication systems, music and acoustics, and medical imaging.